Graph Learning Workshop Notes

Aug 12, 2025

These are notes I wrote after attending Graph Learning Meets Theoretical Computer Science, a workshop at The Simons Institute for the Theory of Computing. Their year-round workshop programming is excellent, they host free conference quality computing research gatherings that you would usually only find at an expensive conference.

The workshop was about machine learning on graphs. Graph models have yet to have their scaling law/chatGPT moment, all the more reason to study them.

Highlights:

• Google's work on graph foundation models for relational databases seems exciting. Convert the db into a graph like so: rows -> nodes, foreign keys -> edges, columns -> features; then predict links with a Graph Neural Network (GNN).
• Learning about model expressivity shocked me, no universal approximation theorem for GNNs!?
• I find the contrast between Message Passing Neural Networks (MPNN) and Graph Transformers to be oddly satisfying — one tackles the graph structure head-on, the other adds it as a little treat.
• Delighted to learn that Graph Transformers often positionally encode nodes with the first few eigenfunctions of the graph laplacian, my love.

Graph Learning

A graph in this context is a collection of nodes, edges connecting two nodes, and optionally features associated with nodes and edges. A feature is any data associated with the node/edge, like a name and an age associated with a graph where nodes represent people.

A graph is a very general object and working with them usually involves making some assumptions about the class of graph you are working with e.g. sparse vs dense graphs or graphs that approximate 3D shapes.

The world is so rich in graph structured information that it's hard to pick representative examples:

Graph learning is concerned with prediction tasks where the input is a graph. This is maybe best understood in contrast to models that operate on images or text. LLMs take in sequences of text tokens, image models like Convolutional Neural Nets or Vision Transformers operate on regular grids of pixels. In both of those cases the input has a natural order and each element has a fixed size neighborhood, there's a natural way to assign coordinates to these inputs. These properties lend themselves to the computationally efficient matrix algebra that has given us the current AI moment.

Graphs on the other hand have no natural ordering of the elements and each element can have varied number of neighbors. Graphs are also permutationally invariant, shuffling the order of the nodes in your graph data structure will create two graphs that have the same underlying structure and models that work with graphs should ideally treat them as identical (see: Graph Isomorphism.)

This irregular structure is more difficult to capture in computationally efficient ways. You can skirt the issue by projecting a graph into the Euclidean plane, the coordinates of which you can feed it into any old neural net; but like in geographic map projection you usually have to sacrifice information to do so (no free lunch.)

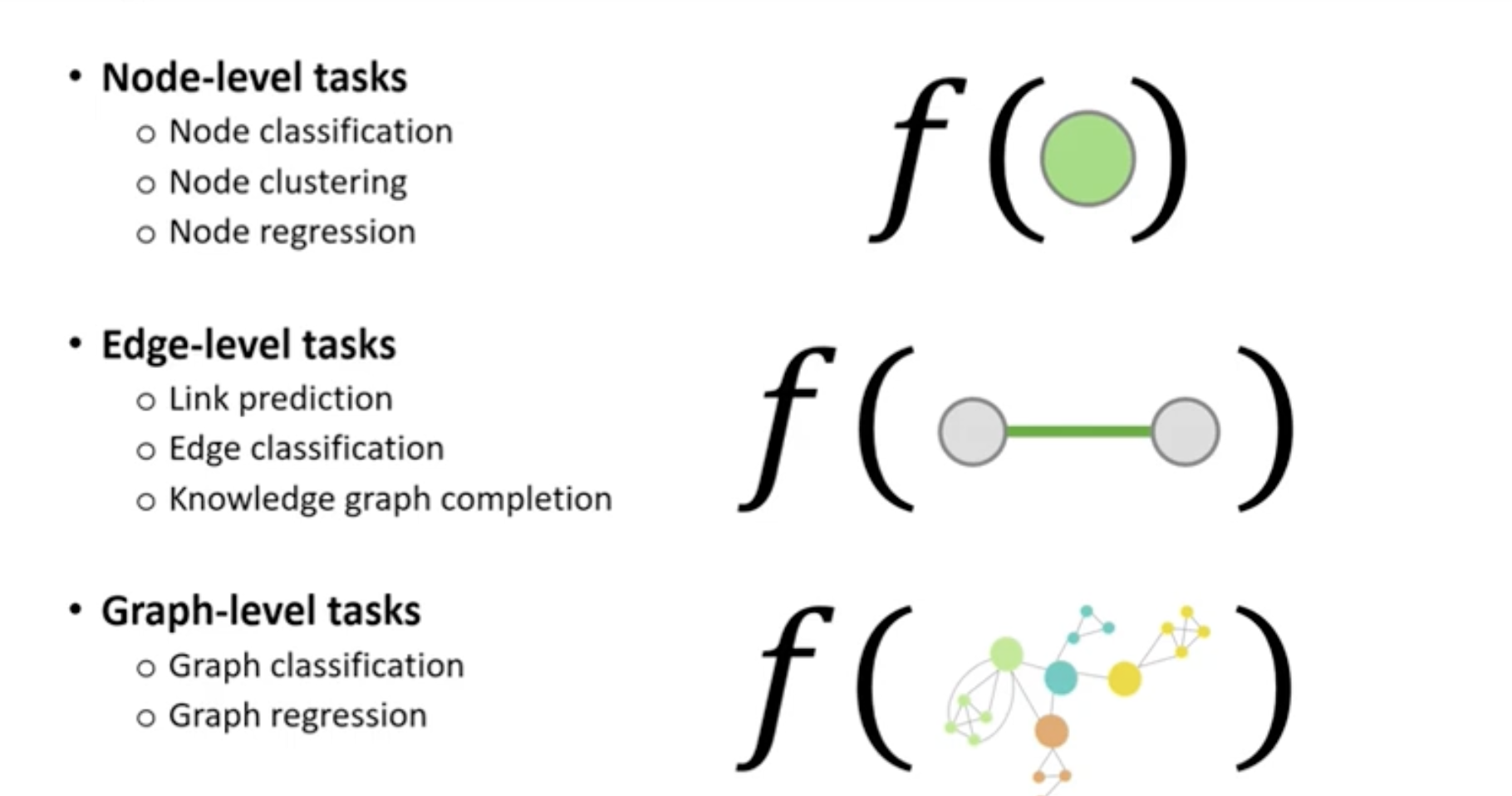
Prediction tasks in Graph Learning

What do we want to accomplish with graph learning? Popular tasks are link prediction, node classification and graph regression.

Many recommendation problems can be cast as link prediction problems, like predicting when two people should be friends in a social network graph. Clearly recommender systems can also be built using traditional regression on tabular data, but to do so information about relationships has to be baked into the input features. The promise of graph learning is that we might be able to leverage the relationship information already inherent to the graph.

Model Architectures

Here are some model architectures specifically for doing prediction tasks on graphs.

Message Passing Neural Net (MPNN)

The first successful GNNs were some flavor of a Message Passing Neural Net (MPNN). MPNNs use the input graph itself as the neural net, very clever. In a traditional Multilayer Perceptron (MLP) the number of nodes per layer and the number of layers are both fixed hyperparameters of the model, and the nodes are fully connected. The network connectivity doesn't change based on the input.

In contrast to an MLP, with MPNN the input graph is the node network. You iterate over the whole graph k times, with each iteration we look at each node and aggregate information from its neighboring nodes. Each full iteration acts like a layer would in a typical MLP and the more layers you have the more information can diffuse around the graph. Each layer is associated with learnable weights that dictate how you combine a node's previous state with the state of its neighbors.

The beauty of this approach is that you are naturally respecting the graph structure, two unconnected nodes can only exchange information as it diffuses through the graph. But the aggregation step is an incredibly local operation and MPNN models cannot efficiently learn about global structure in large graphs. You need at least k layers for the chance that information can diffuse between nodes which are k hops away.

Graph Transformers

Transformer based LLMs are obviously eating the world, can they stomach graphs? Graph transformers take a very different approach from the MPNN and instead feed graphs into a transformer model that operate on sequences of tokens. A preprocessing step adds positional encoding features to each node before it is processed. The encoding features hope to capture and preserve some of the graph connectivity information that is lost when we get rid of the explicit edge connections and just feed the nodes into the model.

This approach lets you lean on the scalability of deep neural nets without completely losing information about the graph topology. Choice of positional encoding plays a big role in how well graph connectivity information is preserved.

Model Expressivity

Now I finally get to describe the fun and surprising thing I learned at this workshop, which had to do with the "expressivity" of graph machine learning models. The expressivity of a model tells you about what kind of functions it's able to approximate.

We know from the universal approximation theorem that an MLP can compute any function, they are fully expressive! It turns out in graph machine learning we are not so fortunate, there are classes of functions that many popular graph model architectures are unable to compute.

Consider these two graphs which are non-isomorphic, certain graph models cannot distinguish between the two. If you squint you can actually see why. Despite having different global connectivity these graphs appear identical from the perspective of each individual node, their differences are invisible to node aggregation style algorithms like MPNN.

Classifying and improving the expressivity of graph models is an area of ongoing research. A benchmark metric, the Weisfeiler-Lehman test, can classify a model as WL-1, WL-2, WL-k etc. and likewise certain graph problems are only solvable if the model is at least WL-n in expressive power. A good example is counting k cycles in the graph, which requires a WL-k model.

Graph mining @ Google

This talk was by Michael Galkin from the Graph Mining team at Google Research.

Graph Foundation Models

Naturally Google is very interested in the possibility of building Graph Foundation Models. These are models which are trained on large corpuses of existing graph data in order to learn how to do link prediction, node classification and graph regression on never before seen graphs. If I understood it right, they aren't training on the content of the training graphs only the structure.

That this would work seems almost unbelievable, an audience member even raised their hand to ask what reasons the author had to expect this to work!

In the LLM case the pre-training step is learning the structure of language, it's not hard to see how an LLM trained on English text would be able to do next token prediction for a sentence in English. With graph foundation models though, you're hoping that the general structure of graphs in one domain can teach you about the structure of graphs in any domain.

Train on social networks and then ask it questions about road networks, do they really have that much in common? Some yet to be published findings on graph foundation models for relational databases would suggest yes. https://research.google/blog/graph-foundation-models-for-relational-data

LLMs for Graphs or Graphs of LLMs

Google has created a fun little distributed systems demo where they task graphs of LLMs with solving classic distributed consensus problems. https://agentsnet.graphben.ch/

In 2025 when you hear people talking about agentic workflows they usually mean something that involve trees of LLMs, with a coordinator at the top. This project on the other hand is about leaderless graphs of LLMs that must figure out how to cooperate. Most aren't that great at it, I kinda wanna see this benchmark run on my friends and I.

Bonus topics

Ok, I think the above was all the good stuff but here are a few other topics that came up.

Equivariant Neural Nets

Equivariance is when a symmetry applied to the model input (e.g. rotation) transforms the output in the same way. Invariance is when a symmetry applied to the input doesn't change the output at all.

The MPNN algorithm is naturally permutation invariant but there are other symmetries it is not invariant or equivariant to.

Imagine a graph which had X,Y,Z positional coordinate features attached to each node, sometimes called a geometric graph. If you rotate the entire graph in space you will end up with a new graph which is isomorphic to the starting graph, ideally graph models which process geometric graphs would be invariant or equivariant to rotation.

I can't pretend to understand how they actually achieved rotational equivariance I got a little lost here.

Graphons?

This 2 hour talk made my head spin. There is an object called a graphon which is almost like an adjacency matrix but it is continuous and for each node position it returns the probability that there is an edge. You can use this as a generative model for graphs of the same family, apparently it only really works well on dense graphs.